Problem Solving and Search

Since puzzles and games have explicit rules, they are often used to explore ideas in artificial intelligence. (Whether the insights thus gained will transfer to less formal domains is another issue...)

A good example of a problem solving domain is the "Tower of Hanoi" puzzle. This puzzle involves a set of three rings of different sizes that can be placed on three different pegs, like so:

In this puzzle, and in other domains where problem solving techniques have been applied, it is convenient to describe the situations that can be encountered while solving the problem as "states". The set of all such states for a given problem is called a "problem space". For the Tower of Hanoi, the problem space is the set of all possible configurations of rings on the pegs.

Some of the configurations or states in the space are given special interpretations:

Initial States
States where a given episode of problem solving starts. In the Tower of Hanoi puzzle, there is one initial state, as shown above. In other domains there may be a number of possible initial states.

Goal or Solution States
States that are considered solutions to the problem. Again, the Tower of Hanoi problem has a single solution state, but usually there are a number of states that count as solutions.

Failure or Impossible States
In some domains, there are states with the property that if they are ever encountered, the problem solving is considered a failure. In the Tower of Hanoi domain, one might define failure states as any in which the rule that rings can only be placed on bigger rings is violated (though it is more common to treat this as a constraint on which operators may be applied, as discussed below).

In some cases these sets are specified explicitly, by describing each state in the set. In other cases the sets of states are specified abstractly.

The characterization of a problem domain also includes the specification of a set of "operators" that can be applied to states in the problem domain. Often a given operator can be applied only to a subset of states in the domain.

In the Tower of Hanoi puzzle, for example, we can consider the set of operators at a state to be the set of possible moves for the each of the top rings. Consider this state of the puzzle:

From this state, there are three operators that can be applied:

1. The red ring can be moved to the right-hand peg.

2. The blue ring can be move to the left-hand peg.

3. The blue ring can be moved to the right-hand peg.

When an operator is applied to a state, it yields a new configuration of the problem domain - a new state.

A sequence of operators that can be performed from a given initial state, that doesn't pass through any failure states, and that leads to a goal state, is called a "solution" to the problem domain.

Search

Generate and Test

	1. generate a potential solution
	2. see if it is in fact a solution
   	   (a) if so stop
           (b) if not, return to 1.

Nevertheless, there are some problem domains where this approach might be used. For example if the set of potential solutions isn't too big, or if it possible to try them quickly, or if the more controlled approaches described below can't be used.

One domain in which pure generate and test is used is by some programs that attempt to break into computer systems. They generate as many passwords or identification codes as they can, until they manage to crack the system, or they are caught or disconnected.

One simple refinement to pure generate and test is to make sure that you don't try the same solution more than once. This is easy if all of the possible solutions can be enumerated - you just try them in order.

If the set of solutions can't be enumerated, another approach is to generate solutions randomly, but to keep a list or an array of all of the solutions you have tried, and before a new one is tried, to see if you have already tried that one.

The problem with this approach is that if it takes you a long time to solve the problem, your list of attempted solutions will grow, and you will spend most of your time checking whether you have tried a given solution before.

If the set of possible solutions is really huge - or if it is infinite - it is best to just generate solutions randomly and not check. The chance of trying something twice is very small, and the overhead of checking is very high.

Random Search

1.  Start with the initial state.
Loop:
   2.a  Choose an operator at random.
   2.b  If the operator can't be applied, 
        or yields a failure state, 
        continue with the previous state at step 2.a.
   2.c  If the result is a goal state, stop.
   2.d  Otherwise, continue with the new state at step 2.a.

1. It might get into an infinite loop generating the same states over and over again.

With generate and test, the problem was that the program might try the same solution repeatedly. Random search is even worse - if the program somehow considers the same problem state twice, it might apply the same operator as it did before, and might then return to that state again and might never even find a whole solution.

As with generate and test, there is no guarantee that this approach will find any solutions, no matter how long it works. As we will see, there are some techniques that can be guaranteed to find a solution if one exists.

There is no way to guarantee that a solution will be found in any particular amount of time, even if it is known that a solution exists. Again, we will see that for some techniques, it is possible to specify how long it will take to find known solutions.

Avoiding the first problem requires that there be some systematic way to explore the state space - at least keeping track of states that have been explored before.

Avoiding the second and third problems requires that the method for determining which states consider is guaranteed (or is at least highly likely) to ultimately result in a solution state.

Most of the details of the search states we will now start discussing can be understood as solutions to these problems with random search.

Search Spaces

Search spaces are often drawn by showing the individual states, with the states that result from applying the domain's operators below them, like this:

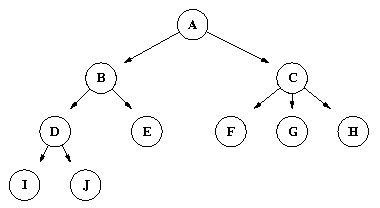
Search spaces for even very simple problems can contain an enormous number of states. Suppose that only two operators apply to each state in the space. In this case the number of states we get by applying operators to the initial states is 2. We have now generated 3 states in the space. Each of the 2 resultant states will yield two more states, so there are 4 states at the next level, yielding a total of 7. The next level has 8, yielding a total of 15 overall and so forth. Here is a picture of the first four levels of a search space, assuming that two operators apply at each state:

The number of states at a level is 2ⁿ, where n is the level of the tree, and the total number of states up to and including level n is 2^(n+1)-1. If there are more operators applicable to each state, each '2' in the above formulae is replaced by the number of operators are applicable.

These formulae are important to remember because they give an idea of how hard the general problem-solving problem is. Here are some values:

	n	2^n		2^(n+1) - 1

	2	4		7
	4	16		31
	6	64		128
	10	1024		2047	
	15	32768		65536
	20	1048576		2097151
	30	1073741824      2147483647

The calculation above does not take into account the fact that applying an operator to a state in the search space might yield a state that is identical to one already in the tree. For some domains this can make a big difference. In the Tower of Hanoi, for example, there are only 72 possible legal states. As we will see, for some search techniques it is important to keep track of which states have been seen before. For others, it is not worth the trouble, and the programs will do fine anyway.

Breadth- and Depth- First Searches

The search space as shown is of course not what a search program starts with. A program will start with the initial state A, and try to find the goal by applying operators to that state, and then to the states B and/or C that result, and so forth. The idea is to find a goal state, and often one is also interested in finding the goal state as fast as possible, or in finding a solution that requires the minimum number of steps, or satisfies some other requirements.

One approach to deciding which states that operators will be applied to is called "Breadth-First Search". In a breadth-first search, all of the states at one level of the tree are considered before any of the states at the next lower level. So for the simple search state pictured above, the states would be applied in the order indicated by the dotted blue line:

Another approach to deciding which states that operators will be applied to is called "Depth-First Search". In a depth-first search, after operators are applied to a state, one of the the resultant states is considered next. So the order in which the states of the simple example space will be considered is:

Also, in this diagram I have assumed that when a state is considered, all of the applicable operators are applied to the state. This isn't always necessary. For example one could apply only one of the possible operators to each node, and then one of the possible operators to the result and so on.

Breadth-First and Depth-First search are sometimes called "blind" or "knowledge-free" search techniques because they incorporate no specific information about the problem domain except that it can be described as a search. We will later discuss how search techniques can take such knowledge into account, often improving the performance of the search program considerably.

These two search techniques have useful properties of their own, and in many cases their simplicity makes them more practical than fancier approaches.

In particular, Breadth-First search can be proved to have the following properties:

1. If a solution exists in the search space, Breadth-First search will (eventually) find it.

2. Breadth-First search will find the shortest possible solution, measured in terms of the number of operator applications.

Depth-First search can't be proved to satisfy either of the above two properties. In particular, if the search space is infinite, Depth-First search might head down one branch of the search tree and never return, even though a solution might exist only a few levels down another branch.

On the other hand, note that for Breadth-First search to find the minimal solution at level N, it must consider at least 2^N search states. This might take a while, if N is very large at all. Suppose that in some search domain there are very many solutions, but all of them are at least 10 levels into the space. Breadth-First search will spend lots of time exploring all of the states at all of the levels below that, while Depth-First search will dive right down to level 10 and presumably find a solution there.

Another case where Depth-First search performs well is when most of the space is failure states, or states where no operators can be applied. In such a search space, it is often best to try sequences of moves until they are known not to work, and then to "backtrack" back to the last legal state.

Also, as we will see next time, Depth-First search can be implemented to run much faster than Breadth-First search.